已知数列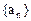 满足
满足 ,求数列
,求数列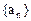 的通项公式。
的通项公式。
已知椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.
(1)求椭圆C的方程;
(2)设椭圆C的左右焦点分别为 ,
,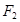 ,过点
,过点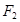 的直线
的直线 与椭圆C交于
与椭圆C交于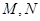 两点.
两点.
①当直线 的倾斜角为
的倾斜角为 时,求
时,求 的长;
的长;
②求 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线 的方程.
的方程.
已知函数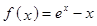 (e为自然对数的底数)
(e为自然对数的底数)
(1)求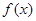 的最小值;
的最小值;
(2)若对于任意的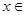
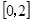 ,不等式
,不等式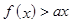 恒成立,求实数
恒成立,求实数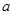 的取值范围.
的取值范围.
如图甲,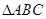 是边长为6的等边三角形,
是边长为6的等边三角形,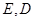 分别为
分别为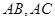 靠近
靠近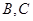 的三等分点,点
的三等分点,点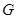 为边
为边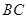 边的中点,线段
边的中点,线段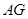 交线段
交线段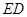 于点
于点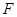 .将
.将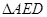 沿
沿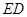 翻折,使平面
翻折,使平面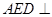 平面
平面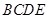 ,连接
,连接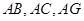 ,形成如图乙所示的几何体.
,形成如图乙所示的几何体.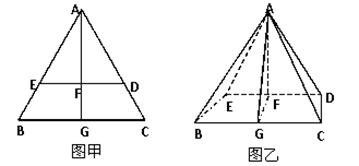
(1)求证: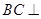 平面
平面
(2)求四棱锥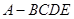 的体积.
的体积.
某地区有小学21所,中学14所,大学7所,现采取分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查。
(1)求应从小学、中学、大学中分别抽取的学校数目;
(2)若从抽取的6所学校中随机抽取2所学校,求抽取的2所学校均为小学的概率.
已知向量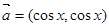 ,
,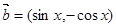 ,设函数
,设函数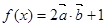 .
.
(1)求函数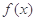 的最小正周期;
的最小正周期;
(2)求函数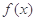 在区间
在区间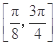 上的最小值和最大值.
上的最小值和最大值.