某运动员训练次数与训练成绩之间的数据关系如下:
| 次数(x) |
30 |
33 |
35 |
37 |
39 |
44 |
46 |
50 |
| 成绩(y) |
30 |
34 |
37 |
39 |
42 |
46 |
48 |
51 |
⑴在图1坐标系中做出散点图;
⑵求出回归方程;
⑶计算相关系数,并利用其检验两个变量的相关关系的显著性;
⑷在图2中做出残差图;
⑸计算相关指数 ;
;
⑹试预测该运动员训练47次及55次的成绩.

正项数列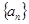 满足
满足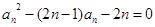 .
.
(1)求数列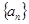 的通项公式;
的通项公式;
(2)令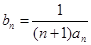 ,求数列
,求数列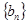 的前
的前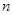 项和
项和 .
.
已知函数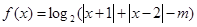 .
.
(1)当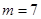 时,求函数
时,求函数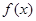 的定义域;
的定义域;
(2)若关于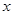 的不等式
的不等式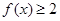 的解集是
的解集是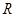 ,求
,求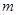 的取值范围.
的取值范围.
已知函数 且
且
(1)试用含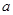 的代数式表示
的代数式表示 ;
;
(2)求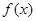 的单调区间;
的单调区间;
(3)令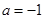 ,设函数
,设函数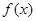 在
在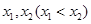 处取得极值,记点
处取得极值,记点 ,证明:线段
,证明:线段 与曲线
与曲线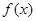 存在异于
存在异于 、
、 的公共点;
的公共点;
椭圆 的离心率为
的离心率为 ,长轴端点A与短轴端点B间的距离为
,长轴端点A与短轴端点B间的距离为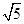 .(1)求椭圆
.(1)求椭圆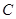 的方程;
的方程;
(2)P为椭圆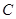 上一动点,求
上一动点,求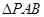 的面积的最大值。
的面积的最大值。
在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为 ,直线L的直角坐标方程为
,直线L的直角坐标方程为 ,且点A在直线L上.
,且点A在直线L上.
(1)求 的值;
的值;
(2)圆C的参数方程为 ,(
,(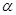 为参数),试判断直线L与圆C的位置关系并说明理由.
为参数),试判断直线L与圆C的位置关系并说明理由.