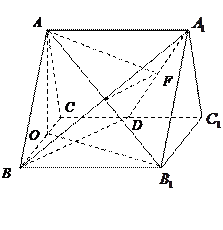 如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。(Ⅰ)求证:AB1⊥面A1BD;
如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点。(Ⅰ)求证:AB1⊥面A1BD;
(Ⅱ)求二面角A-A1D-B的大小;
(Ⅲ)求点C到平面A1BD的距离;
已知函数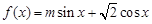 ,
, 的最大值为2.
的最大值为2.
(1)求函数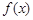 在
在 上的值域;
上的值域;
(2)已知 外接圆半径
外接圆半径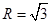 ,
, ,角
,角 所对的边分别是
所对的边分别是 ,求
,求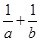 的值.
的值.
已知函数 .
.
(1)若不等式 的解集为
的解集为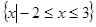 ,求实数a的值;
,求实数a的值;
(2)在(1)的条件下,若存在实数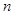 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知直线 :
: 为参数), 曲线
为参数), 曲线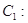
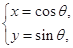 (
( 为参数).
为参数).
(1)设 与
与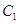 相交于
相交于 两点,求
两点,求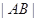 ;
;
(2)若把曲线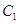 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的
倍,纵坐标压缩为原来的 倍,得到曲线
倍,得到曲线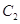 ,设点
,设点 是曲线
是曲线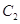 上的一个动点,求它到直线
上的一个动点,求它到直线 的距离的最小值.
的距离的最小值.
已知函数 .
.
(1)求函数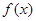 的单调区间;
的单调区间;
(2)若函数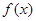 满足:
满足:
①对任意的 ,
, ,当
,当 时,有
时,有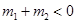 成立;
成立;
②对
 恒成立.求实数
恒成立.求实数 的取值范围.
的取值范围.
我校某同学设计了一个如图所示的“蝴蝶形图案(阴影区域)”来庆祝数学学科节的成功举办.其中 、
、 是过抛物线
是过抛物线 焦点
焦点 的两条弦,且其焦点
的两条弦,且其焦点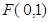 ,
, ,点
,点 为
为 轴上一点,记
轴上一点,记 ,其中
,其中 为锐角.
为锐角.
(1)求抛物线 方程;
方程;
(2)当“蝴蝶形图案”的面积最小时求 的大小.
的大小.