从1,2,3,5,7这五个数字中任取2个,能组成多少个分数?多少个真分数?
(本小题满分14分)直线l过点(1,0),与抛物线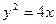 交于A(x1,y1),B(x2,y2)两点,抛物线的顶点是O.
交于A(x1,y1),B(x2,y2)两点,抛物线的顶点是O.
(ⅰ)证明: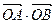 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及l的方程.
(本小题满分14分)已知命题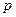 :“函数
:“函数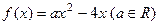 在
在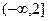 上单调递减”,命题
上单调递减”,命题 :“
:“ ,
,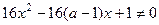 ”,若命题“
”,若命题“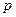 且
且 ”为真命题,
”为真命题,
求实数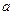 的取值范围。
的取值范围。
.(本小题满分14分) 一个口袋内装有大小相同的6个小球,其中2个红球,记为A1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出的两个球颜色不同的概率.
(本小题满分14分)已知函数 在
在 与
与 时都取得极值
时都取得极值
(1)求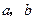 的值;
的值;
(2)若对 ,不等式
,不等式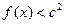 恒成立,求
恒成立,求 的取值范围
的取值范围
(本小题14分) 已知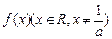 满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使
满足ax·f(x)=2bx+f(x), a≠0, f(1)=1且使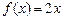 成立的实数x有且只有一个.
成立的实数x有且只有一个.
(1)求 的表达式;
的表达式;
(2)数列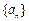 满足:
满足: , 证明:
, 证明: 为等比数列.
为等比数列.
(3)在(2)的条件下, 若 , 求证:
, 求证: