.(本小题满分14分) 一个口袋内装有大小相同的6个小球,其中2个红球,记为A1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出的两个球颜色不同的概率.
已知函数 对于任意的
对于任意的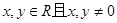 满足
满足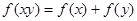 .
.
(1)求 的值;
的值;
(2)求证: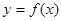 为偶函数;
为偶函数;
(3)若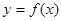 在
在 上是增函数,解不等式
上是增函数,解不等式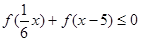
已知函数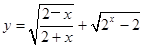 的定义域为
的定义域为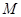 ,
,
(1)求 ;
;
(2)当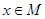 时,求函数
时,求函数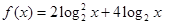 的最大值。
的最大值。
已知函数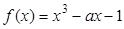 .
.
(Ⅰ)若 在实数集R上单调递增,求
在实数集R上单调递增,求 的范围;
的范围;
(Ⅱ)是否存在实数 使
使 在
在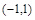 上单调递减.若存在求出
上单调递减.若存在求出 的范围,若不存在说明理由.
的范围,若不存在说明理由.
已知函数f(x)=ax2+2x+c(a、c∈N*)满足:①f(1)=5;②6<f(2)<11.
(1)求a、c的值;
(2)若对任意的实数x∈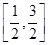 ,都有f(x)-2mx≤1成立,求实数m的取值范围.
,都有f(x)-2mx≤1成立,求实数m的取值范围.
在平面直角坐标系中,以坐标原点为极点, 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为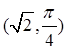 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 在直线上.
在直线上.
(1)求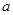 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;
(2)圆c的参数方程为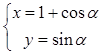 ,(
,(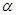 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.