已知点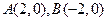 ,
, 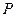 是平面内一动点,直线
是平面内一动点,直线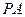 、
、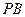 斜率之积为
斜率之积为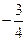 .
.
(Ⅰ)求动点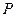 的轨迹
的轨迹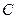 的方程;
的方程;
(Ⅱ)过点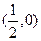 作直线
作直线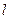 与轨迹
与轨迹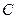 交于
交于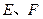 两点,线段
两点,线段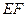 的中点为
的中点为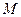 ,求直线
,求直线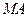 的斜率
的斜率 的取值范围.
的取值范围.
(本小题满分14分)在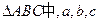 分别是内角A、B、C的对边,已知
分别是内角A、B、C的对边,已知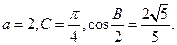
(1)求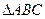 面积;
面积;
(2)设D为AC中点,求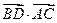 的值。
的值。
(本题满分18分,第(1)小题4分,第(2)小题7分,第(3)小题7分)
对于两个定义域相同的函数 、
、 ,如果存在实数
,如果存在实数 、
、 使得
使得 =
= +
+ ,则称函数
,则称函数 是由“基函数
是由“基函数 、
、 ”生成的.
”生成的.
(1)若 =
= +
+ 和
和 =
= +2生成一个偶函数
+2生成一个偶函数 ,求
,求 的值;
的值;
(2)若 =2
=2 +3
+3 -1由函数
-1由函数 =
= +
+ ,
, =
= +
+

 ,
, ∈R且
∈R且 ≠0
≠0 生成,求
生成,求 +2
+2 的取值范围;
的取值范围;
(3)如果给定实系数基函数 =
= +
+ ,
, =
= +
+

 ≠0
≠0 ,问:任意一个一次函数
,问:任意一个一次函数 是否都可以由它们生成?请给出你的结论并说明理由.
是否都可以由它们生成?请给出你的结论并说明理由.
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)已知直线 :
: =
= +
+

 >0
>0 交抛物线C:
交抛物线C: =2
=2

 >0
>0 于A、B两点,M是线段AB的中点,过M作
于A、B两点,M是线段AB的中点,过M作 轴的垂线交C于点N.
轴的垂线交C于点N.
(1)若直线 过抛物线C的焦点,且垂直于抛物线C的对称轴,试用
过抛物线C的焦点,且垂直于抛物线C的对称轴,试用 表示|AB|;
表示|AB|;
(2)证明:过点N且与AB平行的直线 和抛物线C有且仅有一个公共点;
和抛物线C有且仅有一个公共点;
(3)是否存在实数 ,使
,使 =0.若存在,求出
=0.若存在,求出 的所有值;若不存在,说明理由.
的所有值;若不存在,说明理由.
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
(本题满分14分,第(1)小题6分,第(2)小题8分)
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90 ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.
(1)求四棱锥P-ABCD的体积;
(2)求异面直线PA与BC所成的角.