对于正整数 ,用
,用 表示
表示 的最大奇因数,如:
的最大奇因数,如: ,……. 记
,……. 记 ,其中
,其中 是正整数.
是正整数.
(I)写出 ,
,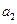 ,
, ,并归纳猜想
,并归纳猜想 与
与
 N)的关系式;
N)的关系式;
(II)证明(I)的结论;
(Ⅲ)求 的表达式.
的表达式.
已知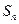 是等差数列
是等差数列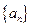 的前
的前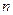 项和,且
项和,且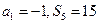 .
.
(1)求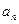 ;
;
(2)令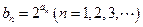 ,计算
,计算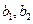 和
和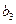 ,由此推测数列
,由此推测数列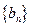 是等差数列还是等比数列,证明你的结论.
是等差数列还是等比数列,证明你的结论.
某商场为经营一批每件进价是10元的小商品,对该商品进行为期5天的市场试销.下表是市场试销中获得的数据.
| 销售单价/元 |
65 |
50 |
45 |
35 |
15 |
| 日销售量/件 |
15 |
60 |
75 |
105 |
165 |
根据表中的数据回答下列问题:
(1)试销期间,这个商场试销该商品的平均日销售利润是多少?
(2)试建立一个恰当的函数模型,使它能较好地反映日销售量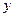 (件)与销售单价
(件)与销售单价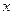 (元)之间的函数关系,并写出这个函数模型的解析式;
(元)之间的函数关系,并写出这个函数模型的解析式;
(3)如果在今后的销售中,该商品的日销售量与销售单价仍然满足(2)中的函数关系,试确定该商品的销售单价,使得商场销售该商品能获得最大日销售利润,并求出这个最大的日销售利润.
如图,在四面体 中,
中, ,
, ,且
,且 分别为
分别为 的中点.
的中点.
(1)求证: ;
;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ∥平面
∥平面 ?证明
?证明 你的结论.
你的结论.
已知两点 ,圆
,圆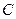 以线段
以线段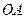 为直径.
为直径.
(1)求圆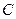 的方程;
的方程;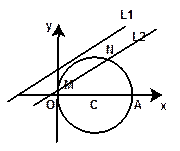 (2)若直线
(2)若直线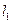 的方程为
的方程为 ,直线
,直线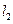 平行于
平行于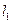 ,且被圆
,且被圆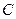 截
截
得的弦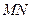 的长是4,求直线
的长是4,求直线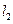 的方程.
的方程.
已知角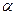 的终边经过点
的终边经过点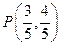 。
。
(1)求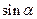 ;
;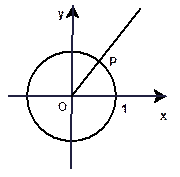 (2)根据上述条件,你能否确定
(2)根据上述条件,你能否确定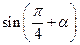 的值?若能,求出
的值?若能,求出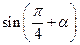
的值;若不能,请说明理由.