(本小题满分14分)已知函数 在
在 与
与 时都取得极值
时都取得极值
(1)求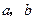 的值;
的值;
(2)若对 ,不等式
,不等式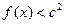 恒成立,求
恒成立,求 的取值范围
的取值范围
几何体EFG —ABCD的面ABCD,ADGE,DCFG均为矩形,AD=DC=l,AE=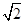 。
。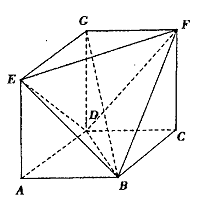
(I)求证:EF⊥平面GDB;
(Ⅱ)线段DG上是否存在点M使直线BM与平面BEF所成的角为45°,若存在求等¥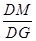 的值;若不存在,说明理由.
的值;若不存在,说明理由.
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为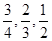 ,乙队每人答对的概率都是
,乙队每人答对的概率都是 .设每人回答正确与否相互之间没有影响,用
.设每人回答正确与否相互之间没有影响,用 表示甲队总得分.
表示甲队总得分.
(I)求随机变量 的分布列及其数学期望E(
的分布列及其数学期望E( );
);
(Ⅱ)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率.
在△ABC中角,A,B,C所对的边分别为a,b,c,向量m=(cos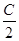 ,1),n=(一l,sin(A+B)),且m⊥n.
,1),n=(一l,sin(A+B)),且m⊥n.
( I)求角C的大小;
(Ⅱ)若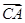 ·
· ,且a+b =4,求c.
,且a+b =4,求c.
已知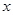 满足不等式
满足不等式 ,求函数
,求函数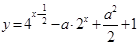 的最小值.
的最小值.
函数
 为奇函数,其图象在点
为奇函数,其图象在点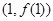 处的切线与直线
处的切线与直线 垂直,导函数
垂直,导函数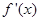 的最小值为
的最小值为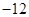 .
.
(1)求 ,
, ,
,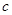 的值;
的值;
(2)求函数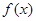 的单调递增区间,并求函数
的单调递增区间,并求函数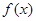 在
在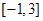 上的最大值和最小值.
上的最大值和最小值.