(本小题满分14分)直线l过点(1,0),与抛物线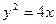 交于A(x1,y1),B(x2,y2)两点,抛物线的顶点是O.
交于A(x1,y1),B(x2,y2)两点,抛物线的顶点是O.
(ⅰ)证明: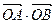 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及l的方程.
已知全集 , 集合
, 集合 ,
,  ,
, .
.
(1)求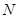 ∩
∩ ;
;
(2)若 ,求实数
,求实数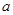 的取值范围.
的取值范围.
某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第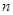 个图形包含
个图形包含 个小正方形.
个小正方形.
(Ⅰ)求出 ;
;
(Ⅱ)利用合情推理的“归纳推理思想”归纳出 与
与 的关系式,并根据你得到的关系式求
的关系式,并根据你得到的关系式求 的表达式.
的表达式.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎), 选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段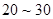 ;
; (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.
(Ⅰ)写出 列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
列联表;判断是否有90%的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)
(Ⅱ)现计划在这次场外调查中按年龄段选取6名选手,并抽取3名幸运奖项, 求至少有一人年龄在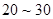 岁之间的概率.
岁之间的概率.
(参考公式 其中
其中 )
)
以直角坐标系原点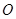 为极点,
为极点, 轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线
轴正半轴为极轴,并在两种坐标系中取相同的长度单位.已知直线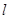 的参数方程为
的参数方程为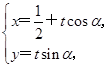 (
( 为参数,
为参数,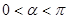 ).曲线
).曲线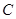 的极坐标方程为
的极坐标方程为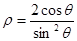
(Ⅰ)求曲线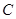 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线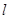 与曲线
与曲线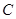 相交于A、B两点,当
相交于A、B两点,当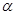 变化时,求
变化时,求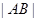 的最小值.
的最小值.
设函数
(Ⅰ)求不等式 的解集
的解集
(Ⅱ)求函数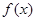 的最小值
的最小值