一种放射性元素,最初的质量为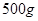 ,按每年
,按每年 衰减.
衰减.
(1)求 年后,这种放射性元素的质量
年后,这种放射性元素的质量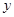 与
与 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的 时所经历的时间).(
时所经历的时间).(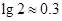 )
)
已知集合 ,集合
,集合 .
.
(1)若 ,求
,求 ;
;
(2)若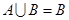 ,求
,求 的取值范围.
的取值范围.
设函数
(Ⅰ)设 ,
,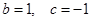 ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;
(Ⅱ)设 ,若对任意
,若对任意
 ,有
,有 ,求
,求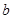 的取值范围
的取值范围
某市电力公司在电力供不应求时期,为了居民节约用电,采用“阶梯电价”方法计算电价,每月用电不超过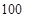 度时,按每度
度时,按每度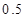 元计费,每月用电超过
元计费,每月用电超过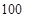 度时,超过部分按每度
度时,超过部分按每度 元计费,每月用电超过
元计费,每月用电超过 度时,超过部分按每度
度时,超过部分按每度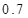 元计费
元计费
(Ⅰ)设每月用电 度,应交电费
度,应交电费 元,写出
元,写出 关于
关于 的函数;
的函数;
(Ⅱ)已知小王家第一季度缴费情况如下:
| 月份 |
1 |
2 |
3 |
合计 |
| 缴费金额 |
87元 |
62元 |
45元8角 |
194元8角 |
问:小王家第一季度共用了多少度电?
已知函数
(Ⅰ)判断函数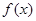 在
在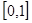 上的单调性,并用定义加以证明;
上的单调性,并用定义加以证明;
(Ⅱ)若对任意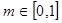 ,总存在
,总存在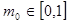 ,使得
,使得 成立,求实数
成立,求实数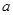 的取值范围
的取值范围