设函数
(Ⅰ)设 ,
,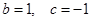 ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;
(Ⅱ)设 ,若对任意
,若对任意
 ,有
,有 ,求
,求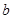 的取值范围
的取值范围
已知直线 过点
过点 与圆
与圆 相切,
相切,
(1)求该圆的圆心坐标及半径长 (2)求直线 的方程
的方程
(满分12分)已知函数 .(Ⅰ) 求
.(Ⅰ) 求 在
在 上的最小值;(Ⅱ) 若存在
上的最小值;(Ⅱ) 若存在 (
( 是常数,
是常数, =2.71828
=2.71828 )使不等式
)使不等式 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ) 证明对一切 都有
都有 成立.
成立.
(满分12分)已知点Pn(an,bn)满足an+1=an·bn+1,bn+1= (n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(2)试用数学归纳法证明:对于n∈N*,点Pn都在(1)中的直线l上.
(满分12分)已知点 ,直线
,直线 :
: 交
交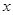 轴于点
轴于点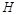 ,点
,点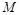 是
是 上的动点,过点
上的动点,过点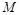 垂直于
垂直于 的直线与线段
的直线与线段 的垂直平分线交于点
的垂直平分线交于点 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;(Ⅱ)若 A、B为轨迹
的方程;(Ⅱ)若 A、B为轨迹 上的两个动点,且
上的两个动点,且 证明直线AB必过一定点,并求出该定点.
证明直线AB必过一定点,并求出该定点.
(满分12分)设函数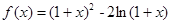 。
。
(Ⅰ)若在定义域内存在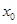 ,而使得不等式
,而使得不等式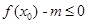 能成立,求实数
能成立,求实数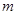 的最小值;
的最小值;
(Ⅱ)若函数 在区间
在区间 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数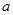 的取值范围。
的取值范围。