已知椭圆
的离心率为
，以原点为圆心，椭圆的短半轴长为半径的圆与直线
相切．
（1）求椭圆
的方程；
（2）若过点
(2，0)的直线与椭圆相交于两点
，设
为椭圆上一点，且满足
（
为坐标原点），求实数
取值范围．
甲居住在城镇的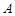
处,准备开车到单位
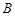处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如：
算作两个路段：路段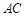
发生堵车事件的概率为
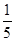,路段
发生堵车事件的概率为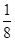
).
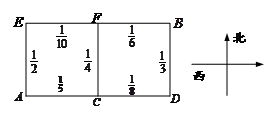
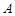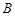(1)请你为甲选择一条由到的最短路线
(即此人只选择从西向东和从南向北的路线),
使得途中发生堵车事件的概率最小；
(2)设甲在路线
中遇到的堵车次数为随机变量
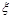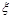,求的数学期望
.
如图示，边长为2的正方形ABCD与正三角形ADP所在平面互相垂直，M是PC的中点。
（1）求证：
∥平面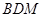
；
（2）求二面角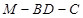
的余弦值。
已知某市2011年新建住房400万平方米，其中有250万平方米是中低价房。预计在今后的若干年内，该市每年新建住房面积平均比上一年增长8％，且每年新建住房中，中低价房的面积均比上一年增加50万平方米。
(1) 到哪一年底，该市历年所建中低价房的累计面积（以2011年为累计的第一年）将首次不少于4750万平方米?
(2) 到哪一年底，该年建造的中低价房的面积占该年建造住房面积的比例首次大于85％?
（参考数据：
）
在
ABC中，a、b、c分别是角 A、B、C所对的边，设
，且
，
。
（1）判断ABC的形状；
（2）
的取值范围。
，求
的最小值。