某城市有甲、乙、丙、丁四个城区,分布如图1-1-3所示,现用五种不同的颜色涂在该城市地图上,要求相邻区域的颜色不相同,不同的涂色方案共有多少种?
已知函数f(x)=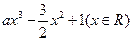 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间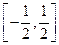 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=错误!不能通过编辑域代码创建对象。,∠BAD=∠CDA=45°.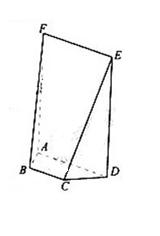
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
设
,
...,
,...是坐标平面上的一列圆,它们的圆心都在
轴的正半轴上,且都与直线
相切,对每一个正整数
,圆
都与圆
相互外切,以
表示
的半径,已知
为递增数列. 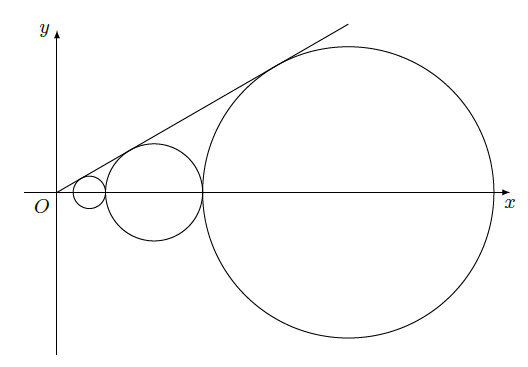
(Ⅰ)证明:
为等比数列;
(Ⅱ)设
=1,求数列
的前
项和.
设函数 ,求函数 的单调区间与极值。
如图,在多面体
中,四边形
是正方形,
为
的中点 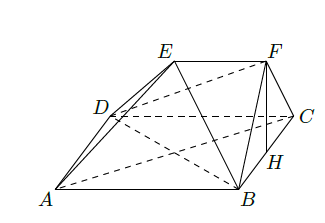
(Ⅰ)求证:
平面
;
(Ⅱ)求证:
平面
;
(Ⅲ)求四面体
的体积;