甲,乙两人进行乒兵球比赛,在每一局比赛中,甲获胜的概率为 。
。
(1)如果甲,乙两人共比赛4局,甲恰好负2局的概率不大于其恰好胜3局的概率,试求 的取值范围;
的取值范围;
(2)若 ,当采用3局2胜制的比赛规则时,求甲获胜的概率;
,当采用3局2胜制的比赛规则时,求甲获胜的概率;
(3)如果甲,乙两人比赛6局,那么甲恰好胜3局的概率可能是 吗?
吗?
已知公差不为0的等差数列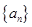 满足
满足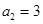 ,
,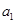 ,
,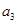 ,
,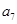 成等比数列.
成等比数列.
(1)求数列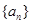 的通项公式;(2)数列
的通项公式;(2)数列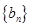 满足
满足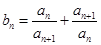 ,求数列
,求数列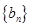 的前
的前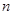 项和
项和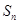 ;(Ⅲ)设
;(Ⅲ)设 ,若数列
,若数列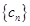 是单调递减数列,求实数
是单调递减数列,求实数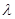 的取值范围.
的取值范围.
已知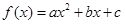 .
.
(1)当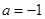 ,
,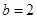 ,
, 时,求
时,求 的解集;
的解集;
(2)当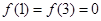 ,且当
,且当 时,
时, 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.
已知圆C经过 两点,且在
两点,且在 轴上截得的线段长为
轴上截得的线段长为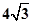 ,半径小于5.(1)求直线
,半径小于5.(1)求直线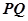 与圆C的方程;(2)若直线
与圆C的方程;(2)若直线 ,直线
,直线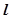 与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线
与圆C交于点A、B,且以AB为直径的圆经过坐标原点,求直线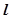 的方程.
的方程.
在△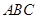 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为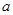 ,
, ,
,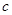 .
.
(1)若 ,求角
,求角 ;
;
(2)若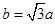 ,
,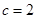 ,且△
,且△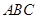 的面积为
的面积为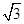 ,求
,求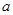 的值.
的值.
设向量a=(2,sinθ),b=(1,cosθ),θ为锐角(1)若a·b=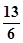 ,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+
,求sinθ+cosθ的值;(2)若a//b,求sin(2θ+ )的值.
)的值.