已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
、(本小题满分12分)
已知向量 ,
,
(1)求 的单调递增区间;
的单调递增区间;
(2)在△ABC中,角A、B、C的对边分别为 ,,
,, ,
,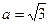 ,B=
,B= ,求b的值。
,求b的值。
(本小题满分12分)已知各项都不相等的等差数列
 的前六项和为60,且
的前六项和为60,且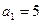 ,
,
(1)求数列 的通项公式
的通项公式 ;
;
(2)若数列 的前
的前 项和
项和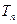 。
。
(本小题满分12分)
已知椭圆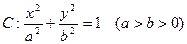 的离心率为
的离心率为 ,过右焦点F的直线
,过右焦点F的直线 与C相交于A、B两点,当直线
与C相交于A、B两点,当直线 的斜率为1时,坐标原点O到
的斜率为1时,坐标原点O到 的距离为
的距离为 。
。
(1)求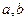 的值;
的值;
(2)椭圆C上是否存在点P,使得当
 绕F转到某一位置时,有
绕F转到某一位置时,有 成立?若存在,求出所有的点P的坐标与
成立?若存在,求出所有的点P的坐标与 的方程;若不存在,说明理由
的方程;若不存在,说明理由
(本小题满分12分)
为了研究某高校大学新生的视力情况,随机地抽查了该校100名进校学生的视力情况,得到频率分布直方图如下图所示,已知后6组的频数从左到右依次是等差数列 的
的 前六项。
前六项。
(1)试确定视力介于4.9至5.0的抽查学生的人数。
(2)若规定视力低于5.0的学生属于近视 学生,试估计该校新生的近视率
学生,试估计该校新生的近视率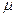 的大
的大
小。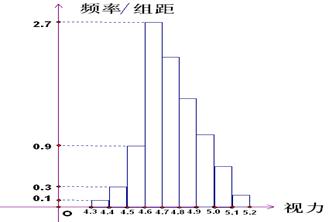
(本小题满分12分)
已知抛物线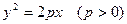 上有一点
上有一点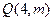 到焦点
到焦点 的距离为5,
的距离为5,
(1)求 及
及 的值。
的值。
(2)过焦点 的直线
的直线 交抛物线于A,B两点,若
交抛物线于A,B两点,若 ,求直线
,求直线 的方程。
的方程。