从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件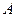 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率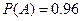 .
.
(1)求从该批产品中任取1件是二等品的概率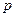 ;
;
(2)若该批产品共100件,从中任意抽取2件,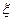 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求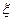 的分布列.
的分布列.
在△ABC中,已知角A为锐角,且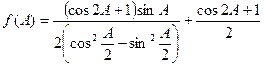 .
.
(1)、将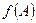 化简成
化简成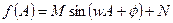 的形式;
的形式;
(2)、若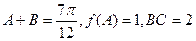 ,求边AC的长. ;
,求边AC的长. ;
设椭圆 过点
过点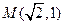 ,离心率为
,离心率为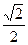
(Ⅰ)求椭圆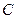 的方程;
的方程;
(Ⅱ)当过点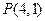 的动直线
的动直线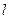 与椭圆
与椭圆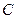 相交与两不同点
相交与两不同点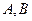 时,在线段
时,在线段 上取点
上取点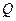 ,满足
,满足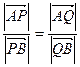 =
=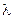 ,证明:点
,证明:点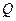 的轨迹与
的轨迹与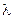 无关.
无关.
已知函数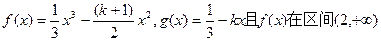 上为增函数.
上为增函数.
(1)求k的取值范围;
(2)若函数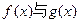 的图象有三个不同的交点,求实数k的取值范围.
的图象有三个不同的交点,求实数k的取值范围.
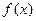 对任意
对任意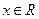 都有
都有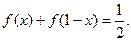
(Ⅰ)求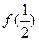 和
和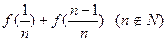 的值;
的值;
(Ⅱ)数列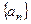 满足:
满足: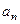 =
=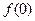 +
+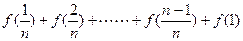 ,数列
,数列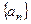 是等差数列吗?请给予证明;
是等差数列吗?请给予证明;
(Ⅲ)令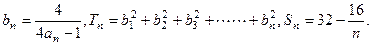
试比较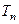 与
与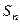 的大小.
的大小.
在三棱柱ABC-A1B1C1中,侧 面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH=
面AA1B1B是边长为2的正方形,点C在平面AA1B1B上的射影H恰好为A1B的中点,且CH= ,设D为
,设D为 中点,
中点,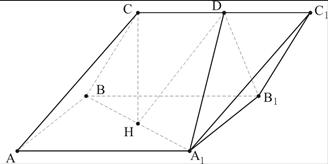
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.