选修4—4:坐标系与参数方程
极坐标系与直角坐标系 有相同的长度单位,以原点为极点,以
有相同的长度单位,以原点为极点,以 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线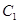 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的参数方程为
的参数方程为 (
( 为参数,
为参数,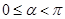 ),射线
),射线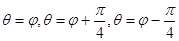 与曲线
与曲线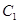 交于(不包括极点O)三点
交于(不包括极点O)三点
(1)求证: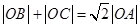 ;
;
(2)当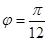 时,B,C两点在曲线
时,B,C两点在曲线 上,求
上,求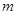 与
与 的值
的值
(本小题14分)(1)写出正弦定理和余弦定理公式;
(2)求和 :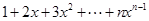
(本小题12分)在△ABC中,BC=a,AC=b,a,b是方程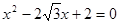 的两个根,且
的两个根,且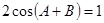 。
。
求:(1)角C的度数;(2)AB的长度。
(本小题12分)设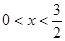 ,求函数
,求函数 的最大值.
的最大值.
(本小题12分)已知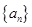 是等差数列,其中
是等差数列,其中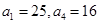
(1)求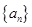 的通项公式;
的通项公式;
(2)数列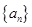 从哪一项开始小于0。
从哪一项开始小于0。
某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取1名,抽到第二批次中女教职工的概率是0.16 .
| 第一批 |
第二批 |
第三批 |
|
| 女 |
196 |
x |
y |
| 男 |
204 |
156 |
z |
(1)求 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3)已知 ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.