已知函数f(x)=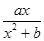 ,且f(x)的图象在x=1处与直线y=2相切.
,且f(x)的图象在x=1处与直线y=2相切.
(1)求函数f(x)的解析式;
(2)若P(x0,y0)为f(x)图象上的任意一点,直线l与f(x)的图象切于P点,求直线l的斜率k的取值范围.
在F1赛车中,赛车位移与比赛时间t存在函数关系s=10t+5t2(s的单位为m,t的单位为s).求:
(1)t=20s,Δt=0.1s时的Δs与 ;
;
(2)t=20s时的瞬时速度.
某一运动物体,在x(s)时离出发点的距离(单位:m)是f(x)=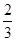 x3+x2+2x.
x3+x2+2x.
(1)求在第1s内的平均速度;
(2)求在1s末的瞬时速度;
(3)经过多少时间该物体的运动速度达到14m/s?
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
设a是实数,讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实数解的个数.