已知关于x的一元二次函数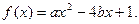
(1)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为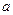 和
和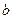 ,求函数
,求函数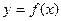 在区间[
在区间[ 上是增函数的概率;
上是增函数的概率;
(2)设点(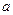 ,
,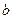 )是区域
)是区域 内的随机点,求函数
内的随机点,求函数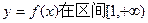 上是增函数的概率.
上是增函数的概率.
(12分)已知函数 ,
,
(1)判断函数 的单调性,并利用单调性定义证明;
的单调性,并利用单调性定义证明;
(2)求函数 的最大值和最小值.
的最大值和最小值.
求 值:
(1) (2)
(2)
(12分)设集合 ,全集为实数集R
,全集为实数集R
(1)求: ;
; ;
;
(2)若 ,求
,求 的取值范围
的取值范围
设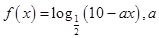 为常数,若
为常数,若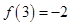 .
.
(1)求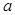 的值;
的值;
(2)求使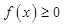 的
的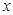 的取值范围;
的取值范围;
(3)若对于区间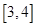 上的每一个
上的每一个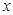 的值,不等式
的值,不等式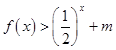 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(本小题满分12分)为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量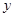 (毫克)与时间
(毫克)与时间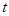 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,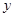 与
与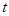 的函数关系式为
的函数关系式为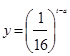 (
(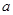 为常数),如图所示.据图中提供的信息,回答下列问题:
为常数),如图所示.据图中提供的信息,回答下列问题: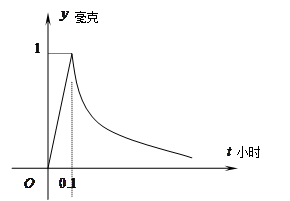
(1)写出从药物释放开始,每立方米空气中的含药量y(毫克)与时间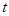 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到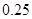 毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?
毫克以下时,学生方可进教室。那么药物释放开始,至少需要经过多少小时后,学生才能回到教室?