用一枚质地均匀的硬币,甲、乙两人做抛掷硬币游戏,甲抛掷4次,记正面朝上的次为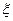 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为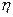 .(Ⅰ)分别求
.(Ⅰ)分别求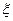 和
和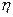 的期望;(Ⅱ)规定:若
的期望;(Ⅱ)规定:若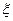 >
>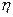 ,则甲获胜;否则,乙获胜.求甲获胜的概率.
,则甲获胜;否则,乙获胜.求甲获胜的概率.
(满分14分)某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.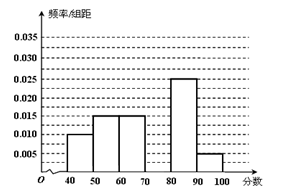
一纸箱中放有除颜色外,其余完全相同的黑球和白球,其中黑球2个,白球3个.
(Ⅰ)从中同时摸出两个球,求两球颜色恰好相同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球颜色恰好不同的概率.
已知 ,
, ,当
,当 为何值时,
为何值时,
(1)  与
与 垂直?(2)
垂直?(2)  与
与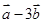 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
在平面直角坐标系中,O为坐标原点,已知向量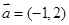 ,又点
,又点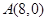 ,
,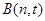 ,
,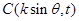 .
.
(1)若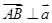 ,且
,且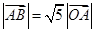 ,求向量
,求向量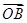 .
.
(2)若向量 与向量
与向量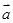 共线,常数
共线,常数 ,当
,当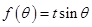 取最大值4时,求
取最大值4时,求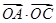 .
.
已知二次函数f(x)=x2+mx+n对任意x∈R,都有f(-x) =f(2+x)成立,设向量 =(sinx,2),
=(sinx,2), =(2sinx,
=(2sinx,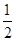 ),
),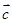 =(cos2x,1),
=(cos2x,1),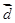 =(1,2),
=(1,2),
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当x∈[0,π]时,求不等式f( ·
· )>f(
)>f(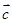 ·
·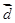 )的解集.
)的解集.