(本题满分13分) 已知椭圆 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过 、
、 、
、 三点. (1)求椭圆
三点. (1)求椭圆 的方程:(2)若点D为椭圆
的方程:(2)若点D为椭圆 上不同于
上不同于 、
、 的任意一点,
的任意一点, ,当
,当 内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线
内切圆的面积最大时。求内切圆圆心的坐标;(3)若直线 与椭圆
与椭圆 交于
交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
(本小题满分12分)
如图,在三棱锥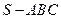 中,侧面
中,侧面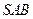
与侧面 均为等边三角形,
均为等边三角形, ,
, 为
为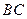 中点.
中点.
(Ⅰ)证明: 平面
平面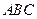 ;(Ⅱ)求二面角
;(Ⅱ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)
在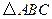 中,已知
中,已知 ,
, ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的值.
的值.
(本小题满分10分)解不等式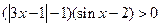
本小题满分14分)已知函数 的图像与函数
的图像与函数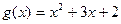 的图象相切,记
的图象相切,记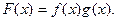
(1)求实数b的值及函数F(x)的极值;
(2)若关于x的方程F(x)=k恰有三个不等的实数根,求实数k的取值范围.
(本小题满分14分)椭圆 的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=
的两个焦点F1、F2,点P在椭圆C上,且P F1⊥PF2,,| P F1|=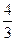 | ,P F2|=
| ,P F2|=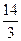 .
.
(I)求椭圆C的方程;
(II)若直线L过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线L的方程。