已知函数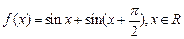 .若
.若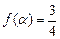 ,求
,求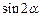 的值.
的值.
已知 是数列
是数列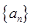 的前
的前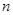 项和,且对任意
项和,且对任意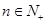 ,有
,有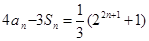 ,
,
求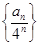 的通项公式;
的通项公式;
求数列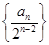 的前
的前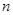 项和
项和 .
.
某医院将一专家门诊已诊的1000例病人的病情及诊断所用时间(单位:分钟)进行了统计,如下表.若视频率为概率,请用有关知识解决下列问题.
| 病症及代号 |
普通病症 |
复诊病症 |
常见病症 |
疑难病症 |
特殊病症 |
| 人数 |
100 |
300 |
200 |
300 |
100 |
| 每人就诊时间(单位:分钟) |
3 |
4 |
5 |
6 |
7 |
用 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求 的数学期望.
的数学期望.
并以此估计专家一上午(按3小时计算)可诊断多少病人;
某病人按序号排在第三号就诊,设他等待的时间为 ,求
,求 ;
;
求专家诊断完三个病人恰好用了一刻钟的概率.
已知直角梯形 中,
中, ,
,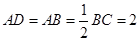 ,
,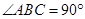 ,
,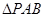 是等边三角形,平面
是等边三角形,平面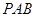 ⊥平面
⊥平面 .
.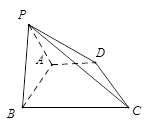
(1)求二面角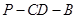 的余弦值;
的余弦值;
(2)求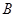 到平面
到平面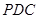 的距离.
的距离.
已知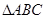 的内角
的内角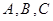 所对边分别为
所对边分别为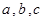 ,且
,且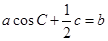 .
.
(1)求角 的大小;
的大小;
(2)若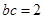 ,求边长
,求边长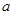 的最小值.
的最小值.
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
(2)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;