已知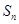 是数列
是数列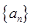 的前
的前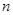 项和,且对任意
项和,且对任意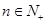 ,有
,有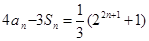 ,
,
求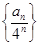 的通项公式;
的通项公式;
求数列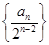 的前
的前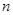 项和
项和 .
.
(本小题满分10分)选修4—4:坐标系与参数方程
以平面直角坐标系的原点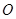 为极点,
为极点, 轴的正半轴为极轴,已知点
轴的正半轴为极轴,已知点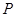 的直角坐标为(1,-5),点
的直角坐标为(1,-5),点 的极坐标为(4,
的极坐标为(4,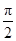 ),若直线
),若直线 过点
过点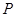 ,且倾斜角为
,且倾斜角为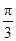 ,圆
,圆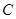 以
以 为圆心,4为半径.
为圆心,4为半径.
(Ⅰ)求直线 的参数方程和圆
的参数方程和圆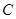 的极坐标方程;
的极坐标方程;
(2)试判定直线 与圆
与圆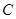 的位置关系.
的位置关系.
(本小题满分10分)选修4—1:几何证明选讲
切线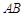 与圆切于点
与圆切于点 ,圆内有一点
,圆内有一点 满足
满足 ,
, 的平分线
的平分线 交圆于
交圆于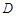 ,
, ,延长
,延长 交圆于
交圆于 ,延长
,延长 交圆于
交圆于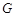 ,连接
,连接 .
.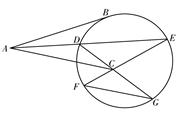
(Ⅰ)证明: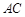 //
// ;
;
(Ⅱ)求证: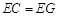 .
.
(本小题满分12分) 已知函数 .
.
(1)若曲线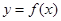 在
在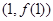 处的切线为
处的切线为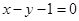 ,求
,求 的值;
的值;
(2)设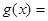
 ,
,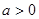 ,证明:当
,证明:当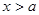 时,
时,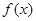 的图象始终在
的图象始终在 的图象的下方;
的图象的下方;
(3)当 时,设
时,设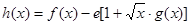 ,(
,(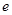 为自然对数的底数),
为自然对数的底数),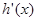 表示
表示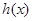 导函数,求证:对于曲线
导函数,求证:对于曲线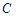 上的不同两点
上的不同两点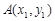 ,
,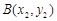 ,
, ,存在唯一的
,存在唯一的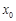
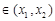 ,使直线
,使直线 的斜率等于
的斜率等于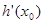 .
.
(本小题满分12分)已知 垂直平分线与
垂直平分线与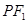 交于Q点.
交于Q点.
(1)求Q点的轨迹方程;
(2)已知点 A(-2,0), 过点 且斜率为
且斜率为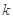 (
(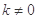 )的直线
)的直线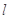 与Q点的轨迹相交于
与Q点的轨迹相交于 两点,直线
两点,直线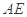 ,
,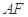 分别交直线
分别交直线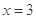 于点
于点 ,
,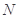 ,线段
,线段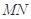 的中点为
的中点为 ,记直线
,记直线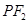 的斜率为
的斜率为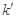 .求证:
.求证: 为定值.
为定值.
(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩共分五组,得到频率分布表如下表所示。

(1)请求出①②位置相应的数字,填在答题卡相应位置上,并补全频率分布直方图;
(2)为了能选出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试,求第3、4、5组中每组各抽取多少人进入第二轮的面试;假定考生“XXX”笔试成绩为178分,但不幸没入选这100人中,那这样的筛选方法对该生而言公平吗?为什么?
(3)在(2)的前提下,学校决定在12人中随机抽取3人接受“王教授”的面试,设第4组中被抽取参加“王教授”面试的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.