一名实习工人用同一台机器制造3个相同的零件,第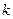 为合格品的概率为
为合格品的概率为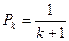 (
(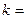 1,2,3),设各次制造的零件合格与否是相互独立的,以
1,2,3),设各次制造的零件合格与否是相互独立的,以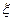 表示合格品的个数,求
表示合格品的个数,求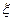 的分布列。
的分布列。
如图,在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=CC1=2。
|
(1)证明:AB1⊥BC1;
(2)求点B到平面AB1C1的距离;本题10分)如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
(1)一条船船顶部宽4m,要使这艘船安全通过,则船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
已知圆C经过A(1, ),B(5,3),并且圆的面积被直线
),B(5,3),并且圆的面积被直线 :
: 平分.求圆C的方程;
平分.求圆C的方程;
已知命题P:方程 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围
已知函数 ,
,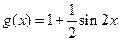 .
.
(1)设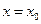 是函数
是函数 图象的一条对称轴,求
图象的一条对称轴,求 的值;
的值;
(2)求函数 的单调递增区间.
的单调递增区间.