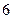 个人坐在一排
个人坐在一排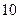 个座位上,问(1)空位不相邻的坐法有多少种?(2)
个座位上,问(1)空位不相邻的坐法有多少种?(2) 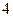 个空位只有
个空位只有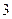 个相邻的坐法有多少种?(3)
个相邻的坐法有多少种?(3) 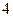 个空位至多有
个空位至多有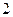 个相邻的坐法有多少种?
个相邻的坐法有多少种?
【2015高考湖北,文22】一种画椭圆的工具如图1所示. 是滑槽
是滑槽 的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且
的中点,短杆ON可绕O转动,长杆MN通过N处铰链与ON连接,MN上的栓子D可沿滑槽AB滑动,且 ,
, .当栓子D在滑槽AB内作往复运动时,带动N绕
.当栓子D在滑槽AB内作往复运动时,带动N绕 转动,M处的笔尖画出的椭圆记为C.以
转动,M处的笔尖画出的椭圆记为C.以 为原点,
为原点, 所在的直线为
所在的直线为 轴建立如图2所示的平面直角坐标系.
轴建立如图2所示的平面直角坐标系.

(Ⅰ)求椭圆C的方程;
(Ⅱ)设动直线 与两定直线
与两定直线 和
和 分别交于
分别交于 两点.若直线
两点.若直线 总与椭圆
总与椭圆 有且只有一个公共点,试探究:
有且只有一个公共点,试探究: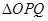 的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
【2015高考福建,文19】已知点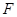 为抛物线
为抛物线 的焦点,点
的焦点,点 在抛物线
在抛物线 上,且
上,且 .
.
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)已知点 ,延长
,延长 交抛物线
交抛物线 于点
于点 ,证明:以点
,证明:以点 为圆心且与直线
为圆心且与直线 相切的圆,必与直线
相切的圆,必与直线 相切.
相切.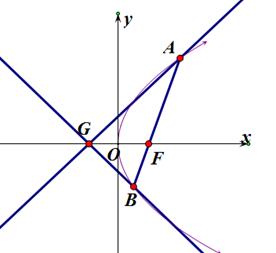
【2015高考北京,文20】(本小题满分14分)已知椭圆
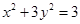 ,过点
,过点 且不过点
且不过点 的直线与椭圆
的直线与椭圆 交于
交于 ,
, 两点,直线
两点,直线 与直线
与直线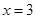 交于点
交于点 .
.
(Ⅰ)求椭圆 的离心率;
的离心率;
(Ⅱ)若 垂直于
垂直于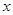 轴,求直线
轴,求直线 的斜率;
的斜率;
(Ⅲ)试判断直线 与直线
与直线 的位置关系,并说明理由.
的位置关系,并说明理由.
【2015高考安徽,文20】设椭圆E的方程为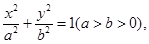 点O为坐标原点,点A的坐标为
点O为坐标原点,点A的坐标为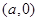 ,点B的坐标为(0,b),点M在线段AB上,满足
,点B的坐标为(0,b),点M在线段AB上,满足 直线OM的斜率为
直线OM的斜率为 .
.
(Ⅰ)求E的离心率e;
(Ⅱ)设点C的坐标为(0,-b),N为线段AC的中点,证明:MN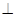 AB.
AB.
【2015高考新课标1,文20】(本小题满分12分)已知过点 且斜率为k的直线l与圆C:
且斜率为k的直线l与圆C: 交于M,N两点.
交于M,N两点.
(Ⅰ)求k的取值范围;
(Ⅱ) ,其中O为坐标原点,求
,其中O为坐标原点,求 .
.