在研究某种新措施对猪白痢的防治效果问题时，得到了以下数据：
| |
存活数 |
死亡数 |
合计 |
| 新措施 |
132 |
18 |
150 |
| 对照 |
114 |
36 |
150 |
| 合计 |
246 |
54 |
300 |
试利用图形和独立性检验来判断新措施对防治猪白痢是否有效？
（本小题满分12分）
已知
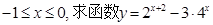的最大值和最小
值.
（本小题满分12分）
两城相距
，在两地之间距
城
的
地建一核电站给两城供电，为保证城市安全，核电站距市距离不得少于
．已知供电费用与供电距离的平方和供电量之积成正比，比例系数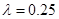
．若城供电量为
亿度/月，
城为
亿度/月．
（I）把月供电总费用
表示成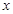
的函数，并求定义域；
（II）核电站建在距城多远，才能使供电费用最小．
（本小题满分12分）直线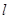
经过点
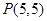，且与圆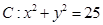
相交，截得弦长为
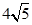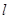，求的方程．
（本小题满分12分）如图是一个几何体的正视图和俯视图.
（I）画出其侧视图，试判断该几何体是什么几何体；
（II）求出该几何体的全面积；
（III）求出该几何体的体积.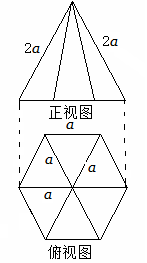
（本小题满分12分）求经过两直线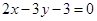
和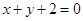
的交点且与直线
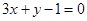垂直的直线方程．