(本小题满分12分)求经过两直线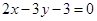 和
和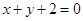 的交点且与直线
的交点且与直线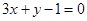 垂直的直线方程.
垂直的直线方程.
(选修4-4;坐标系与参数方程)已知直线 经过点P(1,1),倾斜角
经过点P(1,1),倾斜角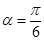 ,
,
(1)写出直线 的参数方程;
的参数方程;
(2)设 与圆
与圆 相交与两点A、B,求点P到A、B两点的距离之积.
相交与两点A、B,求点P到A、B两点的距离之积.
(本小题满分12分)已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1,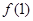 )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在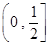 上至少存在一个实数
上至少存在一个实数 ,使
,使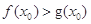 成立,求正实数
成立,求正实数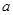 的取值范围.
的取值范围.
(本小题满分12分)已知数列 ,
, 满足
满足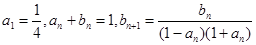 .
.
(1)求 ;
;
(2)设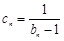 ,证明数列
,证明数列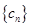 是等差数列;
是等差数列;
(3)设 ,不等式
,不等式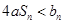 恒成立时,求实数
恒成立时,求实数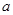 的取值范围.
的取值范围.
(本小题满分12分)平面直角坐标系 中,椭圆C:
中,椭圆C: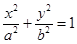 (
(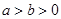 )的离心率为
)的离心率为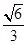 ,焦点为
,焦点为 、
、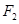 ,直线
,直线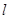 :
: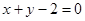 经过焦点
经过焦点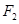 ,并与C相交于A、B两点.
,并与C相交于A、B两点.
(1)求C的方程;
(2)在C上是否存在C、D两点,满足 ∥
∥ ,
,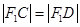 ,若存在,求直线
,若存在,求直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分)如图,直四棱柱 的底面是菱形,侧面是正方形,
的底面是菱形,侧面是正方形,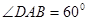 ,
,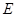 是棱
是棱 的延长线上一点,经过点
的延长线上一点,经过点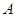 、
、 、
、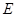 的平面交棱
的平面交棱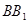 于点
于点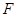 ,
, .
.
(1)求证:平面 平面
平面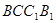 ;
;
(2)求二面角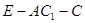 的余弦值.
的余弦值.