本小题满分12分)
某电视 台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
| 文艺节目 |
新闻节目 |
总计 |
|
| 20至40岁 |
40 |
18 |
58 |
| 大于40岁 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(1)由表中数据直观分析,收看新闻节目的观众是否与年龄有关?
(2)用分层抽样方法在收看新闻节目的观众中随机抽取5名,大于40岁的观众应抽取几名?
(3)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为20至40岁的概率。
(满分12分)已知函数 在
在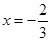 与
与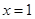 时都取得极值
时都取得极值
(1)求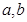 的值与函数
的值与函数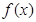 的单调区间
的单调区间
(2)若对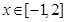 ,不等式
,不等式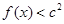 恒成立,求
恒成立,求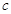 的取值范围。
的取值范围。
(满分12分)已知四棱锥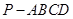 的底面为直角梯形,
的底面为直角梯形,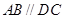 ,
,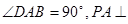 底面
底面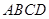 ,且
,且 ,
,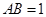 ,
, 是
是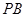 的中点。
的中点。
(Ⅰ)证明:面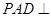 面
面 ;
;
(Ⅱ)求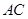 与
与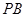 所成的角;
所成的角;
(Ⅲ)求面 与面
与面 所成二面角的余弦值。
所成二面角的余弦值。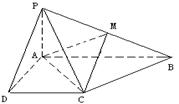
.4.命题 方程
方程 有两个不等的正实数根,命题
有两个不等的正实数根,命题 方程
方程 无实数根。若“
无实数根。若“ 或
或 ”为真命题,求
”为真命题,求 的取值范围。
的取值范围。
(本小题满分14分)
设函数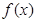 对任意实数
对任意实数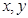 都有
都有 且
且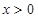 时
时 。
。
(Ⅰ)证明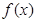 是奇函数;
是奇函数;
(Ⅱ)证明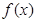 在
在 内是增函数;
内是增函数;
(Ⅲ)若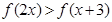 ,试求
,试求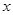 的取值范围。
的取值范围。