(本小题满分12分)已知全集 ,集合
,集合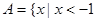 或
或 ,
,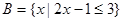 .
.
求:(1)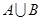 (2)
(2)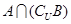 (3)
(3)  .
.
已知二次函数f(x)的最小值为1,且f(0)=f(2)=3.
(1)求f(x)的解析式.
(2)若f(x)在区间[2a,a+1]上不单调,求实数a的取值范围.
(3)在区间[-1,1]上,y=f(x)的图象恒在y=2x+2m+1的图象上方,试确定实数m的取值范围.
已知函数f(x)= 
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
已知函数f(x-1)=x2-4x,求函数f(x),f(2x+1)的解析式.
若集合A={x|x2+x-6=0},B={x|x2+x+a=0},且B⊆A,求实数a的取值范围.