(本小题满分14分)
如图,在 ,已知A(-
,已知A(- ,0), B(
,0), B( ,0), CD
,0), CD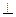 AB于D,
AB于D,  的垂心为H,且
的垂心为H,且
(Ⅰ)求点H的轨迹方程;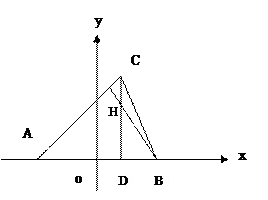
(Ⅱ)若过定点F(0,2)的直线交曲线 于不同的两点
于不同的两点 (点
(点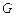 在F,H之间),且满足
在F,H之间),且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分13分)
已知函数 ,且对于任意实数
,且对于任意实数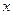 ,恒有
,恒有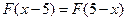 。
。
(1)求函数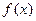 的解析式;
的解析式;
(2)已知函数 在区间
在区间 上单调,求实数
上单调,求实数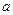 的取值范围;
的取值范围;
(3)函数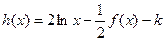 有几个零点?
有几个零点?
. (本小题满分12分)
数列 满足
满足 ,
,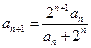 (
(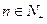 ).
).
(Ⅰ)证明:数列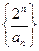 是等差数列;
是等差数列;
(Ⅱ)求数列 的通项公式
的通项公式 ;
;
(Ⅲ)设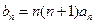 ,求数列
,求数列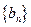 的前
的前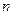 项和
项和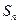 .
.
(本小题满分12分)
已知直角梯形 中,
中,  ,
,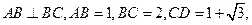 过
过 作
作 ,垂足为
,垂足为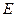 ,
,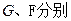
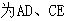 的中点,现将
的中点,现将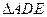 沿
沿 折叠,使得
折叠,使得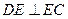 .
.
(1)求证: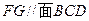 ;
;
(2)设四棱锥D-ABCE的体积为V,其外接球体积为 ,求V
,求V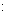
 的值.
的值.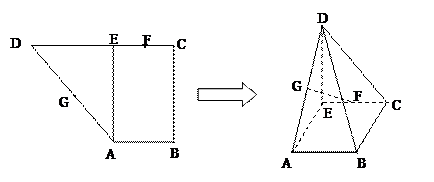

(本小题满分12分)已知集合 ,
, .
.
(1)在区间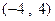 上任取一个实数
上任取一个实数 ,求“
,求“ ”的概率;
”的概率;
(2)设 为有序实数对,其中
为有序实数对,其中 是从集合
是从集合 中任取的一个整数,
中任取的一个整数, 是从集合
是从集合 中任取的一个整数,求“
中任取的一个整数,求“ ”的概率.
”的概率.