(本小题满分14分)
如图,在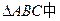 ,已知A(-
,已知A(- ,0), B(
,0), B( ,0), CD
,0), CD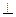 AB于D,
AB于D, 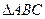 的垂心为H,且
的垂心为H,且
(Ⅰ)求点H的轨迹方程;
(Ⅱ)若过定点F(0,2)的直线交曲线 于不同的两点
于不同的两点 (点
(点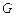 在F,H之间),且满足
在F,H之间),且满足 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知函数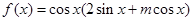 的图象经过点
的图象经过点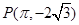 .
.
(Ⅰ)求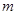 的值以及
的值以及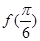 ;
;
(Ⅱ)函数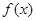 的图象向右平移
的图象向右平移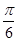 后得到函数
后得到函数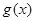 的图象,求
的图象,求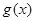 在
在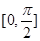 上的值域.
上的值域.
(本小题满分14分)已知函数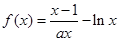 (
(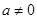 )
)
(Ⅰ)求函数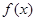 的单调区间;
的单调区间;
(Ⅱ)当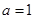 时,求
时,求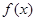 在
在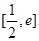 上的最大值和最小值(
上的最大值和最小值( );
);
(Ⅲ)求证: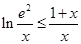 .
.
(本小题满分13分)已知中心在原点,对称轴为坐标轴的椭圆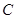 的一个焦点
的一个焦点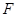 在抛物线
在抛物线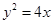 的准线上,且椭圆
的准线上,且椭圆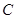 过点
过点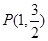 ,直线
,直线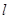 与椭圆
与椭圆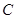 交于
交于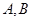 两个不同点.
两个不同点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线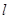 的斜率为
的斜率为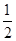 ,且不过点
,且不过点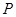 ,设直线
,设直线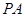 ,
,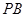 的斜率分别为
的斜率分别为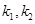 ,求证:
,求证: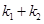 为定值;
为定值;
(Ⅲ)若直线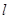 过点
过点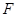 ,
,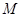 为椭圆
为椭圆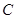 的另一个焦点,求
的另一个焦点,求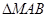 面积的最大值.
面积的最大值.
(本小题满分12分)已知等差数列 单调递增,且
单调递增,且  ,
, 都在函数
都在函数 的图象上.
的图象上.
(Ⅰ)求数列 的通项公式和前
的通项公式和前 项和为
项和为 ;
;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分10分)学校足球队进行罚点球训练,队员在一轮训练中最多可罚4次,并规定,一旦命中该队员即停止此轮练习,否则一直罚到第4次为止. 已知一选手罚点球的命中率为0.8,求一轮练习中,该选手的实际罚球次数X的分布列,并求X的数学期望.