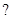设函数 .若方程
.若方程 的根为
的根为 和
和 ,
,
且 .
.
(1)求函数 的解析式;
的解析式;
(2)已知各项均不为零的数列 满足:
满足:  (
( 为该数列前
为该数列前 项和),求该数列的通项
项和),求该数列的通项 .
.
.已知函数f(x)=lg[(a2-1)x2+(a+1)x+1],若f(x)的定义域为R,求实数a的取值范围.
已知y=loga(2-ax)在区间{0,1}上是x的减函数,求a的取值范围.
设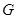 、
、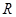 分别为不等边
分别为不等边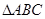 的重心与外心
的重心与外心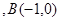 、
、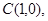 且
且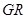 平行于
平行于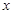
轴
(1)求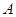 点的轨迹
点的轨迹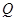 的方程
的方程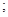
(2)是否存在直线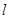 过点
过点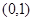 并与曲线
并与曲线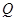 交于
交于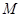 、
、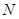 两点
两点 且以
且以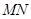 为直径的
为直径的
圆过坐标原点 若存在
若存在 求出直线
求出直线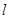 的方程
的方程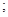 若不存在
若不存在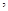 请说明理由
请说明理由
已知函数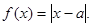
(1)若不等式 的解集为
的解集为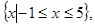 求实数
求实数 的值
的值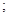
(2)在(1)的条件下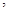 若
若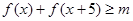 对一切实数
对一切实数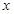 恒成立
恒成立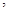 求实数
求实数 的
的
取值范围
某车间小组共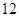 人
人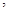 需配置两种型号的机器
需配置两种型号的机器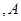 型机器需
型机器需 人操作
人操作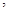 每天耗
每天耗
电 能生产出价值
能生产出价值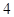 万元的产品
万元的产品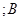 型机器需
型机器需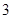 人操作
人操作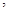 每天耗电
每天耗电 能生产出价值
能生产出价值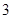 万元的产品现每天供应车间的电能不多于
万元的产品现每天供应车间的电能不多于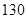
 问该车间小组应如何配置两种型号的机器
问该车间小组应如何配置两种型号的机器 才能使每天的产值最
才能使每天的产值最
大 最大值是多少
最大值是多少