如图甲,在平面四边形ABCD中,已知
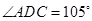 ,
,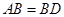 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD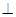 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
(Ⅰ)求证:DC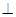 平面ABC;
平面ABC;
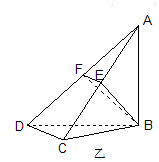
(Ⅱ)设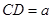 ,求三棱锥F-ABE的体积.
,求三棱锥F-ABE的体积.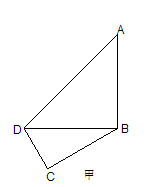
已知集合A={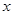 |
|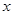 ≤
≤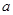 +3},B={
+3},B={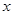 |
|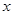 <-1或
<-1或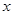 >5}.
>5}.
(1) 若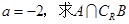 ;(2) 若
;(2) 若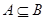 ,求
,求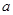 的取值范围.
的取值范围.
求下列各式的值: (1)
(1)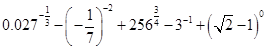
 (2)
(2)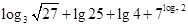
已知函数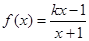 ,且函数
,且函数 是
是 上的增函数。
上的增函数。
(1)求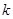 的取值范围;
的取值范围;
(2)若对任意的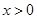 ,都有
,都有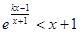 (e是自然对数的底),求满足条件的最大整数
(e是自然对数的底),求满足条件的最大整数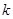 的值。
的值。
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
 |
3 |
 2 2 |
4 |
 |
 |
 |
0 |
 4 4 |
 |
(Ⅰ)求 的标准方程;
的标准方程;
(Ⅱ)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。