已知一动直线 与两坐标轴的正半轴围成的三角形的面积的数值比直线
与两坐标轴的正半轴围成的三角形的面积的数值比直线 的纵、横截距之和大1,求这三角形面积的最小值.
的纵、横截距之和大1,求这三角形面积的最小值.
已知a,b是不相等的正数,在a,b之间分别插入m个正数a1,a2, ,am和正数b1,b2, ,
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5, =
=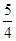 ,求
,求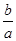 的值;
的值;
(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
已知函数f(x)=lnx-mx(m R).
R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
已知椭圆C: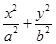 =1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=
=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c= b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
(1)求椭圆C的方程;
(2)若直线l1的斜率为-1,求△PMN的面积;
(3)若线段MN的中点在x轴上,求直线MN的方程.
某种树苗栽种时高度为A(A为常数)米,栽种n年后的高度记为f(n).经研究发现f(n)近似地满足 f(n)=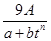 ,其中
,其中 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
(1)栽种多少年后,该树木的高度是栽种时高度的8倍;
(2)该树木在栽种后哪一年的增长高度最大.
如图,在四棱锥P-ABCD中,O为AC与BD的交点,AB^平面PAD,△PAD是正三角形,
DC//AB,DA=DC=2AB.
(1)若点E为棱PA上一点,且OE∥平面PBC,求 的值;
的值;
(2)求证:平面PBC^平面PDC.