已知函数f(x)=lnx-mx(m R).
R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
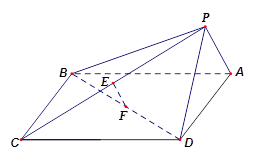
如图,在四棱锥 中,底面
中,底面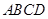 是正方形,侧面
是正方形,侧面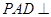 底面
底面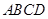 .
.
(Ⅰ)若 ,
, 分别为
分别为 ,
,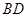 中点,求证:
中点,求证: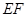 ∥平面
∥平面 ;
;
(Ⅱ)求证: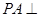
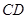 ;
;
(Ⅲ)若 ,求证:平面
,求证:平面 平面
平面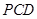 .
.
某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(Ⅱ)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
在 中,
中, ,
,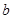 ,
,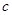 分别是角
分别是角 的对边.已知
的对边.已知 ,
,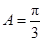 .
.
(1)若 ,求角
,求角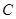 的大小;
的大小;
(2)若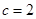 ,求边
,求边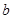 的长.
的长.
已知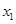 ,
,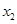 是函数
是函数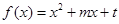 的两个零点,其中常数
的两个零点,其中常数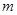 ,
,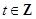 ,设
,设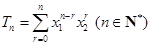 .
.
(Ⅰ)用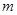 ,
,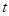 表示
表示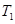 ,
,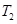 ;
;
(Ⅱ)求证: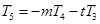 ;
;
(Ⅲ)求证:对任意的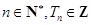 .
.
已知椭圆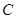 的中心在原点
的中心在原点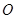 ,焦点在
,焦点在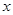 轴上,离心率为
轴上,离心率为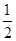 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为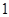 .
.
(Ⅰ)求椭圆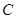 的标准方程;
的标准方程;
(Ⅱ)是否存在与椭圆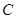 交于
交于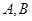 两点的直线
两点的直线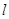 :
: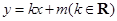 ,使得
,使得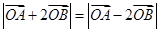 成立?若存在,求出实数
成立?若存在,求出实数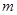 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.