某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分为150分),将成绩按如下方式分成六组,第一组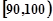 、第二组
、第二组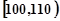 、第六组
、第六组 . 下图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
. 下图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
(Ⅰ)求第四和第五组频率,并补全频率分布直方图;
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面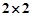 列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
列联表(即填写空格处的数据),并判断是否有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
| |
 |
 |
合计 |
| 参加培训 |
5 |
|
8 |
| 未参加培训 |
|
|
|
| 合计 |
|
4 |
|
附:
 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)
已知 ,
, (ω>0),函数
(ω>0),函数 的最小正周期为π
的最小正周期为π
(1) 求函数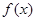 的单调递减区间及对称中心;
的单调递减区间及对称中心;
(2) 求函数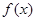 在区间
在区间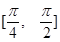 上的最大值与最小值.
上的最大值与最小值.
(本小题满分12分)
已知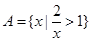 ,
,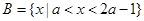 ,a∈R,若“x∈A”是“x∈B”的必要条件,求a的取值范围
,a∈R,若“x∈A”是“x∈B”的必要条件,求a的取值范围
(本小题满分10分)
已知等差数列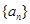 中,
中, ,
,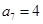 ,
,
(1) 求数列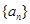 的通项公式; (2) 求数列
的通项公式; (2) 求数列 的前20项的和.
的前20项的和.
(本小题满分12分)
已知函数
(1)求 的单调区间;
的单调区间;
(2)设 ,若对任意
,若对任意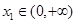 ,均存在
,均存在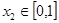 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知 F1、F2是椭圆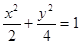 的两焦点,
的两焦点, 是椭圆在第一象限弧上一点,且满足
是椭圆在第一象限弧上一点,且满足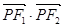 =1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
=1.过点P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标;
(2)求证直线AB的斜率为定值;
(3)求△PAB面积的最大值.