已知椭圆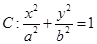
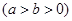 的离心率为
的离心率为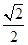 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线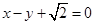 相切.
相切.
(Ⅰ)求椭圆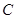 的方程;
的方程;
(Ⅱ)若过点 的直线与椭圆
的直线与椭圆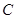 相交于两点
相交于两点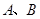 ,设
,设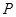 为椭圆上一点,且满足
为椭圆上一点,且满足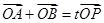 (其中
(其中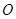 为坐标原点),求整数
为坐标原点),求整数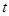 的最大值.
的最大值.
(本小题满分15分)
在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式 分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图。
在选取的40名学生中。
(I)求成绩在区间 内的学生人数;
内的学生人数;
(II)从成绩大于等于80分的学生中随机选2名学生,求至少有1名学生成绩在区间[90,100]内的概率。
(本小题满分12分)
在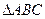 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为
(I)求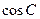 的值;
的值;
(II)若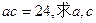 的值。
的值。
(本小题满分14分)
在数列 和
和 中,已知
中,已知 ,其中
,其中 且
且 。
。
(I)若 ,求数列
,求数列 的前n项和;
的前n项和;
(II)证明:当 时,数列
时,数列 中的任意三项都不能构成等比数列;
中的任意三项都不能构成等比数列;
(III)设集合 ,试问在区间[1,a]上是否存在实数b使得
,试问在区间[1,a]上是否存在实数b使得 ,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
,若存在,求出b的一切可能的取值及相应的集合C;若不存在,说明理由。
(本小题满分14分) 椭圆
椭圆 短轴的左右两个端点分别为A,B,直线
短轴的左右两个端点分别为A,B,直线 与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
与x轴、y轴分别交于两点E,F,交椭圆于两点C,D。
(I)若 ,求直线
,求直线 的方程;
的方程;
(II)设直线AD,CB的斜率分别为 ,若
,若 ,求k的值。
,求k的值。
(本小题满分13分)
已知 ,函数
,函数 ,记曲线
,记曲线 在点
在点 处切线为
处切线为 与x轴的交点是
与x轴的交点是 ,O为坐标原点。
,O为坐标原点。
(I)证明:
(II)若对于任意的 ,都
,都 有
有 成立,求a的取值范围。
成立,求a的取值范围。