分别指出由下列各组命题构成的逻辑关联词“或”、“且”、“非”的真假。
(1)p: 梯形有一组对边平行;q:梯形有一组对边相等。
(2)p: 1是方程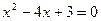 的解;q:3是方程
的解;q:3是方程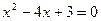 的解。
的解。
(3)p: 不等式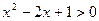 解集为R;q: 不等式
解集为R;q: 不等式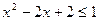 解集为
解集为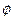 。
。
(4)p: 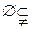
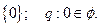
如图,动点 与两定点 、 构成 ,且直线 的斜率之积为4,设动点 的轨迹为 。
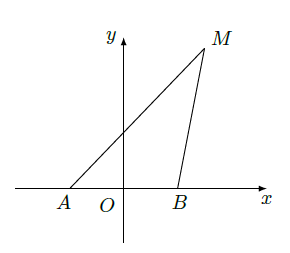
(Ⅰ)求轨迹
的方程;
(Ⅱ)设直线
与
轴交于点
,与轨迹
相交于点
,且
,求
的取值范围。
已知数列
的前
项和为
,常数
,且
对一切正整数
都成立.
(Ⅰ)求数列
的通项公式;
(Ⅱ)设
,
,当
为何值时,数列
的前
项和最大?
如图,在三棱锥 中, , , ,点 在平面 内的射影 在 上。
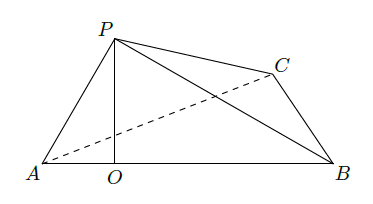
(Ⅰ)求直线
与平面
所成的角的大小;
(Ⅱ)求二面角
的大小。
已知函数
.
(Ⅰ)求函数
的最小正周期和值域;
(Ⅱ)若
,求
的值.
某居民小区有两个相互独立的安全防范系统(简称系统)
和
,系统
和系统
在任意时刻发生故障的概率分别为
和
。
(Ⅰ)若在任意时刻至少有一个系统不发生故障的概率为
,求的
值;
(Ⅱ)求系统 在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率。