已知函数 ,
, ,
,
 的最小值恰好是方程
的最小值恰好是方程 的三个根,其中
的三个根,其中 .求证:
.求证: ;
;
设椭圆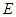 :
: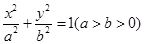 的左、右焦点分别为
的左、右焦点分别为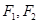 ,已知椭圆
,已知椭圆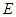 上的任意一点
上的任意一点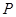 ,满足
,满足 ,过
,过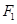 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.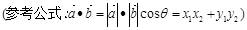
(1)求椭圆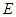 的方程;
的方程;
(2)若过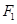 的直线交椭圆于
的直线交椭圆于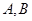 两点,求
两点,求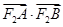 的取值范围.
的取值范围.
袋子里有大小相同但标有不同号码的3个红球和4个黑球,从袋子里随机取出4个球.
⑴求取出的红球数的概率分布列;
⑵若取到每个红球得2分,取到每个黑球得1分,求得分不超过5分的概率.
已知函数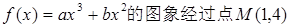 ,曲线在点M处的切线恰好与直线
,曲线在点M处的切线恰好与直线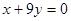 垂直。
垂直。
(1)求实数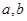 的值;
的值;
(2)若函数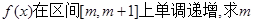 的取值范围。
的取值范围。
求二项式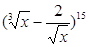 的展开式中:
的展开式中:
(1)常数项(答案可保留组合数);(2)有几个有理项;(3)有几个整式项.
有9名学生,其中2名会下象棋但不会下围棋,3名会下围棋但不会下象棋,4名既会下围棋又会下象棋;现在要从这9名学生中选出2名学生,一名参加象棋比赛,另一名参加围棋比赛,共有多少种不同的选派方法?