（本小题满分14分）已知等比数列
的前
项和为
（Ⅰ）求数列的通项公式；
（Ⅱ）设数列
满足
，
为数列 的前项和，试比较
与 
的大小，并证明你的结论．
已知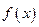
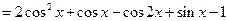
（1）求函数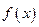最小正周期；
（2）当
，求函数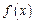
的最大值及取得最大值时的
；
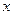数列{an}是等差数列，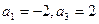
。
（1）求通项公式an
（2）若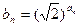
，求数列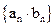
的前n项和Sn
（本小题满分10分）
选修4－5：不等式选讲
已知函数
．
（1）作出函数
的图像；
（2）解不等式
．
（本小题满分10分）
选修4—1：几何证明选讲
如图，AB是⊙O的直径，C，F为⊙O上的点，CA是∠BAF的角平分线，过点C作
CD⊥AF交AF的延长线于D点，CM⊥AB，垂足为点M.
（1）求证：DC是⊙O的切线；
（2）求证：AM·MB=DF·DA.
已知函数
（
）．
（1）当
时，求函数
在
上的最大值和最小值；
（2）当函数在
单调时，求
的取值范围；
（3）求函数既有极大值又有极小值的充要条件。