如图所示,F1、F2是双曲线x2 – y2 = 1的两个焦点,O为坐标原点,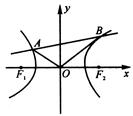
圆O是以F1F2为直径的圆,直线l:y = kx + b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当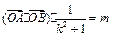 ,且满足2≤m≤4时,
,且满足2≤m≤4时,
求△AOB面积的取值范围.
设集合A={x| },B={x|
},B={x| 或
或 }.分别求满足下列条件的实数m的取值范围:
}.分别求满足下列条件的实数m的取值范围:
(1) ;
;
(2) .
.
(本小题满分13分)已知二次函数 对任意实数
对任意实数 都满足
都满足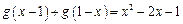 ,且
,且 .令
.令 .
.
(1)求 的表达式;
的表达式;
(2)设 ,
, ,证明:对任意
,证明:对任意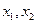
 ,恒有
,恒有
(本小题满分13分)某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率 ,例如:
,例如: .
.
(1)求 ;
;
(2)求第 个月的当月利润率
个月的当月利润率 ;
;
(3)该企业经销此产品期间,哪个月的当月利润率最大,并求该月的当月利润率.
(本小题满分13分)设数列 是公比大于1的等比数列,
是公比大于1的等比数列, 为其前
为其前 项和,已知
项和,已知 =7且
=7且 ,
, ,
, 成等差数列.
成等差数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列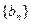 的前
的前 项和
项和 
(3)求 的表达式.
的表达式.
(本小题满分12分)如图,四棱锥 的底面是正方形,
的底面是正方形, ,点E在棱PB上.
,点E在棱PB上.
(1)求证:平面 ;
;
(2)当 且E为PB的中点时,
且E为PB的中点时,
求AE与平面PDB所成的角的大小.