(本小题满分14分)数列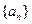 和数列
和数列 由下列条件确定:
由下列条件确定:
① ;
;
②当 时,
时,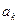 与
与 满足如下条件:当
满足如下条件:当 时,
时,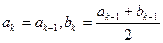 ;当
;当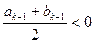 时,
时, 。
。
解答下列问题:
(Ⅰ)证明数列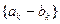 是等比数列;
是等比数列;
(Ⅱ)求数列 的前n项和为
的前n项和为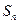 ;
;
(Ⅲ)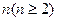 是满足
是满足 的最大整数时,用
的最大整数时,用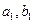 表示n的满足的条件。
表示n的满足的条件。
已知椭圆: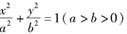 与X轴、y轴的正半轴分别交于A,B两点,原点O到直线AB的距离为
与X轴、y轴的正半轴分别交于A,B两点,原点O到直线AB的距离为 ,该椭圆的离心率为
,该椭圆的离心率为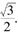
(I)求椭圆的方程;
(II)是否存在过点 的直线I与椭圆交于M,N两个不同的点,且对l外任意一点Q,有
的直线I与椭圆交于M,N两个不同的点,且对l外任意一点Q,有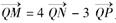 成立?若存在,求出l的方程;若不存在,说明理由.
成立?若存在,求出l的方程;若不存在,说明理由.
某幼儿园为训练孩子的数字运算能力,在一个盒子里装有标号为1,2,3,4,5的卡片各2张,让孩子从盒子里任取3张卡片,按卡片上最大数字的9倍计分,每张卡片被取出的可能性都相等,用X表示取出的3张卡片上的最大数字.
(I)求取出的3张卡片上的数字互不相同的概率;
(II)求随机变量x的分布列及数学期望;
(III)若孩子取出的卡片的计分超过30分,就得到奖励,求孩子得到奖励的概率.
如图,已知直角梯形ACDE所在的平面垂直于平面ABC,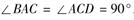 ,
,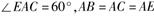
(I )在直线BC上是否存在一点P,使得DP//平面EAB?请证明你的结论;
(II)求平面EBD与平面ABC所成的锐二面角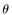 的余弦值.
的余弦值.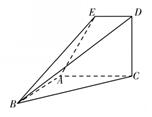
已知数列 的前n项和为
的前n项和为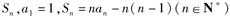 .
.
(I)求数列 的通项公式;
的通项公式;
(II)设 ,求数列
,求数列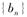 的前n项和Tn
的前n项和Tn
设函数 .
.
(1)求曲线 在点
在点 处的切线方程;(2)求函数
处的切线方程;(2)求函数 的单调区间;
的单调区间;
(3)若函数 在区间
在区间 内单调递增,求
内单调递增,求 的取值范围.
的取值范围.