已知函数 ,
, 为函数
为函数 的导函数.
的导函数.
(Ⅰ)若数列 满足:
满足: ,
, (
(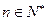 ),求数列
),求数列 的通项
的通项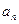 ;
;
(Ⅱ)若数列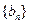 满足:
满足: ,
, (
(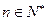 ).
).
ⅰ.当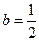 时,数列
时,数列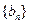 是否为等差数列?若是,请求出数列
是否为等差数列?若是,请求出数列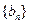 的通项
的通项 ;若不是,请说明理由;
;若不是,请说明理由;
ⅱ.当 时, 求证:
时, 求证: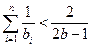 .
.
某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量 与产量
与产量 之间的关系式为
之间的关系式为 ,每件产品的售价
,每件产品的售价 与产量
与产量 之间的关系式为
之间的关系式为 .
.
(Ⅰ)写出该陶瓷厂的日销售利润 与产量
与产量 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
如图,已知在直四棱柱 中,
中, ,
,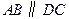 ,
,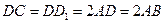
 .
.
(I)求证: 平面
平面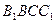 ;
;
(II)求二面角 的余弦值.
的余弦值.
甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是 ,甲、乙、丙三人都能通过测试的概率是
,甲、乙、丙三人都能通过测试的概率是 ,甲、乙、丙三人都不能通过测试的概率是
,甲、乙、丙三人都不能通过测试的概率是 ,且乙通过测试的概率比丙大.
,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;
(Ⅱ)求测试结束后通过的人数 的数学期望
的数学期望 .
.
在△ABC中,A、B、C的对边分别为a、b、c,
(1)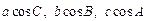 成等差数列.求B的值;
成等差数列.求B的值;
(2)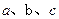 成等比数列. 求角B的取值范围;
成等比数列. 求角B的取值范围;
设函数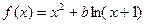 .
.
(1)若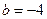 ,求函数
,求函数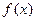 的单调区间;
的单调区间;
(2)若函数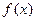 在定义域上是单调函数,求
在定义域上是单调函数,求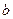 的取值范围;
的取值范围;
(3)若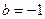 ,证明对任意
,证明对任意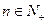 ,不等式
,不等式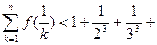 …
…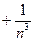 都成立。
都成立。