设函数f(x)=loga(x-3a)(a>0且a≠1),当点P(x,y)是函数y=f(x)图像上的点时,点Q(x-2a,-y)是函数y=g(x)图像上的点.
(1)写出函数y=g(x)的解析式;
(2)若当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
(本小题满分12分)
某学生在上学路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是 ,遇到红灯时停留的时间都是
,遇到红灯时停留的时间都是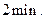
(Ⅰ)求这名学生在上学路上到第三个路口时首次遇到红灯的概率;
(Ⅱ)这名学生在上学路上因遇到红灯停 留的总时间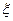 的分布列及期望
的分布列及期望
(本小题满分12分)
已知函数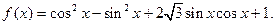
(Ⅰ)求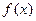 的最小正周期,并求
的最小正周期,并求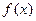 的最小值;
的最小值;
(Ⅱ)若 =2,且
=2,且 ,求
,求 的值
的值
(本小题满分12分)
对于函数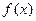 ,若存在
,若存在 R,使
R,使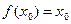 成立,则称
成立,则称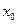 为
为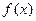 的不动点.如果函数
的不动点.如果函数 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且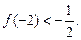
(1)求实数 ,
,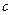 的值;
的值;
(2)已知各项不为零的数列
 ,并且
,并且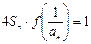 , 求数列
, 求数列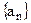 的通项公式;;
的通项公式;;
(3)求证: .
.
(本小题满分12分)
已知F1、F2分别是双曲线x2-y2=1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y=kx+b (b>0)与圆O相切,并与双曲线相交于A、B两点.
(Ⅰ)根据条件求出b和k满足的关系式;
(Ⅱ)向量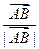 在向量
在向量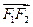 方向的投影是p,当(×)p2=1时,求直线l的方程;
方向的投影是p,当(×)p2=1时,求直线l的方程;
(Ⅲ)当(×)p2=m且满足2≤m≤4时,求DAOB面积的取值范围.
(本小题满分12分)
已知双曲线 的离心率为
的离心率为 ,右准线方程为
,右准线方程为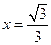
(Ⅰ)求双曲线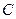 的方程;
的方程;
(Ⅱ)设直线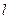 是圆
是圆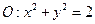 上动点
上动点 处的切线,
处的切线,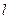 与双曲线
与双曲线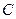 交于不同的两点
交于不同的两点 ,证明
,证明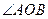 的大小为定值.
的大小为定值.