某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).
(1)把y表示成x的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时,既符合上面的两个条件,又能使净收入最多?
在四棱锥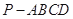 中,侧面
中,侧面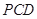
 底面
底面 ,
, ,底面
,底面 是直角梯形,
是直角梯形,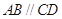 ,
, ,
, ,
,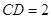 .
.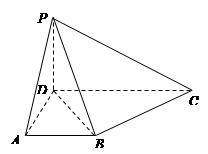
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)设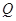 为侧棱
为侧棱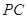 上一点,
上一点,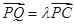 ,试确定
,试确定 的值,使得二面角
的值,使得二面角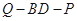 为
为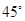 .
.
在进行一项掷骰子放球的游戏中规定:若掷出1点或2点,则在甲盒中放一球;否则,在乙盒中放一球。现在前后一共掷了4次骰子,设 、
、 分别表示甲、乙盒子中球的个数。
分别表示甲、乙盒子中球的个数。
(Ⅰ)求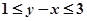 的概率;
的概率;
(Ⅱ)若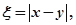 求随机变量
求随机变量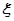 的分布列和数学期望。
的分布列和数学期望。
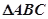 的三个内角A,B,C所对的边分别为a,b,c, 向量
的三个内角A,B,C所对的边分别为a,b,c, 向量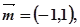
 且
且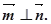
(Ⅰ)求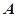 的大小;
的大小;
(Ⅱ)现给出下列四个条件:①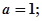 ②
②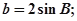 ③
③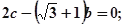 ④
④ .试从中再选择两个条件以确定
.试从中再选择两个条件以确定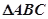 ,求出你所确定的
,求出你所确定的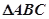 的面积.
的面积.
近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨。现由天气预报得知,某地在未来3天的指定时间的降雨概率是:前2天均为50%,后1天为80%.3天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.求不需要人工降雨的天数x的分布列和期望.
某服装商场为了了解毛衣的月销售量 (件)与月平均气温
(件)与月平均气温 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温 |
17 |
13 |
8 |
2 |
月销售量 (件) (件) |
24 |
33 |
40 |
55 |
(1)做出散点图;
(2) 求线性回归方程 ;
;
(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(  ,
, )
)