定义在(－1，1)上的函数f(x)满足①对任意x、y∈(－1,1),都有f(x)+f(y)=f(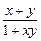
);②当x∈(－1,0)时，有f(x)>0.
求证: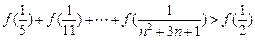
.
设
，其中a∈R，曲线y=f(x)在点(1，f(1))处的切线与y轴相交于点(0，6)．
(1)确定a的值;
(2)求函数f(x)的单调区间与极值．
已知函数
．
(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性;
(2)当m≤2时，证明f(x)>0．
如图,AB为⊙O的直径,直线CD与⊙O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连结AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.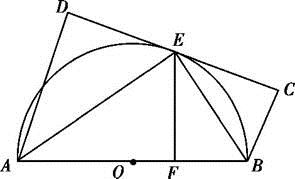
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC=
,延长CE交AB于点F,求△BCF外接圆的半径.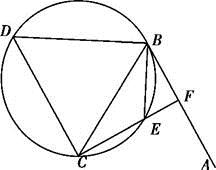
已知函数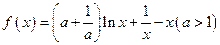
．
（1）讨论f(x)在区间（0，1）上的单调性；
（2）当a∈[3，+∞)时，曲线
上总存在相异的两点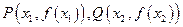
，使得曲线在点P，Q处的切线互相平行，求证：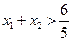
．