设数列{an}的前n项和Sn=na+n(n-1)b,(n=1,2,…),a、b是常数且b≠0.
(1)证明:{an}是等差数列.
(2)证明:以(an,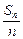 -1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
-1)为坐标的点Pn(n=1,2,…)都落在同一条直线上,并写出此直线的方程.
(3)设a=1,b=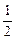 ,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
,C是以(r,r)为圆心,r为半径的圆(r>0),求使得点P1、P2、P3都落在圆C外时,r的取值范围.
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。分别从甲、乙两组中各抽取2名工人进行技术考核。每此抽取互不影响。
(1)求从甲组抽取的工人中恰有1名女工人的概率;
(2)求抽取的4名工人中恰有2名男工人的概率..
(满分14分)
某地区的农产品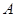 第
第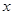 天
天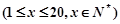 的销售价格
的销售价格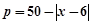 (元∕百斤),一农户在第
(元∕百斤),一农户在第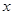 天
天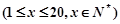 农产品
农产品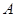 的销售量
的销售量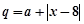 (百斤)(
(百斤)(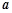 为常数),且该农户在第7天销售农产品
为常数),且该农户在第7天销售农产品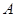 的销售收入为2009元。
的销售收入为2009元。求该农户在第10天销售农产品
 的销售收入是多少?
的销售收入是多少?这20天中该
 农户在哪一天的销售收入最大?为多少?
农户在哪一天的销售收入最大?为多少?
设
,点
的坐标为
,点
在抛物线
上运动,点
满足
,经过
点与
轴垂直的直线交抛物线于点
,点
满足
,求点
的轨迹方程。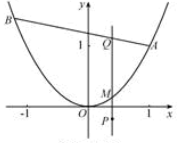
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果前一个人10分钟内不能完成任务则撤出,再派下一个人,现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别 ,假设 互不相等,且假定各人能否完成任务的事件相互独立。
(Ⅰ)如果按甲最先、乙次之、丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为 ,其中 是 的一个排列,求所需派出人员数目 的分布列和均值(数学期望) ;
(Ⅲ)假定
,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数学期望)达到最小.
(Ⅰ)设 , ,证明: .
(Ⅱ) ,证明: .