在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.
(1)若D是BC的中点,求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,求证:截面MBC1⊥侧面BB1C1C;
(3)AM=MA1是截面MBC1⊥平面BB1C1C的充要条件吗?请你叙述判断理由.
如图5,已知直角梯形 所在的平面垂直于平面
所在的平面垂直于平面 ,
, ,
, ,
,
 .
.
(1)在直线 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?请证明你的结论;
?请证明你的结论;
(2)求平面 与平面
与平面 所成的锐二面角
所成的锐二面角 的余弦值。
的余弦值。
(本题满分12分) 已知平面区域 恰好被面积最小的圆C:
恰好被面积最小的圆C: 及其内部覆盖.
及其内部覆盖.
(1)求圆C的方程;
(2)斜率为1的直线 与圆C交于不同两点A、B,且
与圆C交于不同两点A、B,且 ,求直线
,求直线 的方程.
的方程.
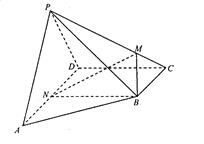
如图,四棱锥P-ABCD的侧面PAD垂直于底面ABCD,∠ADC=∠BCD=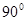 ,PA=PD=AD=2BC=2,CD
,PA=PD=AD=2BC=2,CD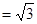 ,M在棱PC上,N是AD的中点,二面角M-BN-C为
,M在棱PC上,N是AD的中点,二面角M-BN-C为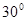 .
.
(1)求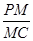 的值;
的值;
(2)求直线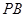 与平面BMN所成角的正弦值.
与平面BMN所成角的正弦值.
已知 ,且
,且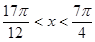 ,
,
求 ①  的值;
的值;
② 的值。
的值。
已知函数 的图象在
的图象在 轴上的截距为1,它在
轴上的截距为1,它在 轴右侧的第一个最大值点和最小值点分别为
轴右侧的第一个最大值点和最小值点分别为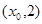 和
和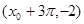 .
.
(1)试求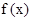 的解析式;
的解析式;
(2)将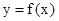 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的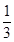 (纵坐标不变),然后再将新的图象向
(纵坐标不变),然后再将新的图象向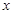 轴正方向平移
轴正方向平移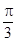 个单位,得到函数
个单位,得到函数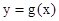 的图象.求出函数
的图象.求出函数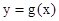 的解析式。
的解析式。