设数列 的前
的前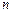 项和为
项和为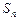 ,已知
,已知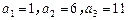 ,且
,且 ,
,
其中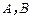 为常数.
为常数.
(Ⅰ)求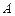 与
与 的值;
的值;
(Ⅱ)证明:数列 为等差数列;
为等差数列;
(Ⅲ)证明:不等式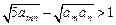 对任何正整数
对任何正整数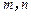 都成立.
都成立.
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为,|OB|=2,设∠AOB=θ,θ∈.
(1)用θ表示点B的坐标及|OA|;
(2)若tanθ=-,求O·O的值.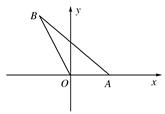
如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?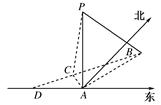
在△ABC中,BC=,AC=3,sinC=2sinA.
(1)求AB的值;
(2)求sin的值.
在△ABC中,角A,B,C的对边分别为a,b,c,已知a+b=5,c=,且cos 2C+2cos(A+B)=-.
(1)求角C的大小;
(2)求△ABC的面积S.
设a=(-1,1),b=(4,3),c=(5,-2)
(1)求证:a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求λ1和λ2,使c=λ1a+λ2b.