如图,在海岛A上有一座海拔1千米的山,山顶设有一个观察站P,上午11时,测得一轮船在岛北偏东30°,俯角为30°的B处,到11时10分又测得该船在岛北偏西60°,俯角为60°的C处.
(1)求船的航行速度是每小时多少千米?
(2)又经过一段时间后,船到达海岛的正西方向的D处,问此时船距岛A有多远?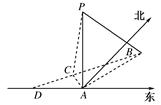
如图,地图上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高位10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.
(1)若圆形标志物半径为25m,以PG所在直线为X轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即 )的正切值为
)的正切值为 ,求该圆形标志物的半径.
,求该圆形标志物的半径.
已知直线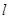 与圆
与圆 相交于A,B两点,弦AB的中点为
相交于A,B两点,弦AB的中点为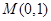
(1)求实数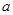 的取值范围以及直线
的取值范围以及直线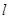 的方程;
的方程;
(2)若以AB为直径的圆过原点O,求圆C的方程.
在 中,
中, ,D是边BC上一点,
,D是边BC上一点,
(1)求 的值;
的值;
(2)求 的值
的值
已知函数 (其中
(其中 为常数,且
为常数,且 )的部分图像如图所示.
)的部分图像如图所示.
(1)求函数 的解析式
的解析式
(2)若 求
求 的值
的值
选修4-5:不等式选讲
设函数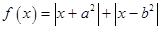 ,其中
,其中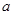 ,
, 为实数.
为实数.
(1)若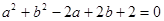 ,解关于
,解关于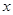 的不等式
的不等式 ;
;
(2)若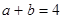 ,证明:
,证明: